Деформированное упругое тело (например, растянутая или сжатая пружина) способно, возвращаясь в недеформированное состояние, совершить работу над соприкасающимися с ним телами. Следовательно, упруго деформированное тело обладает потенциальной энергией. Она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина, зависит от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к нерастянутому состоянию, т. е. найдем потенциальную энергию растянутой пружины.
Пусть растянутая пружина закреплена одним концом, а второй конец, перемещаясь, совершает работу. Нужно учитывать, что сила, с которой действует пружина, не остается постоянной, а изменяется пропорционально растяжению. Если первоначальное растяжение пружины, считая от нерастянутого состояния, равнялось , то первоначальное значение силы упругости составляло , где - коэффициент пропорциональности, который называют жесткостью пружины. По мере сокращения пружины эта сила линейно убывает от значения до нуля. Значит, среднее значение силы равно . Можно показать, что работа равна этому среднему, умноженному на перемещение точки приложения силы:
Таким образом, потенциальная энергия растянутой пружины
Такое же выражение получается для сжатой пружины.
В формуле (98.1) потенциальная энергия выражена через жесткость пружины и через ее растяжение . Заменив на , где - упругая сила, соответствующая растяжению (или сжатию) пружины , получим выражение
которое определяет потенциальную энергию пружины, растянутой (или сжатой) силой . Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, т.е. чем больше ее упругость, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной растягивающей, силе. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на перемещение точки приложения силы, т. е. работа.
Эта закономерность имеет большое значение, например, при устройстве различных рессор и амортизаторов: при посадке на землю самолета амортизатор шасси, сжимаясь, должен произвести большую работу, гася вертикальную скорость самолета. В амортизаторе с малой жесткостью сжатие будет больше, зато возникающие силы упругости будут меньше и самолет будет лучше предохранен от повреждений. По той же причине при тугой накачке шин велосипеда дорожные толчки ощущаются резче, чем при слабой накачке.
Энергией называется скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие.
Для характеристики различных форм движения материи вводятся соответствующие виды энергии, например: механическая, внутренняя, энергия электростатических, внутриядерных взаимодействий и др.
Энергия подчиняется закону сохранения, который является одним из важнейших законов природы.
Механическая энергия Е характеризует движение и взаимодействие тел и является функцией скоростей и взаимного расположения тел. Она равна сумме кинетической и потенциальной энергий.
Кинетическая энергия
Рассмотрим случай, когда на тело массой m действует постоянная сила \(~\vec F\) (она может быть равнодействующей нескольких сил) и векторы силы \(~\vec F\) и перемещения \(~\vec s\) направлены вдоль одной прямой в одну сторону. В этом случае работу силы можно определить как A = F ∙s . Модуль силы по второму закону Ньютона равен F = m∙a , а модуль перемещения s при равноускоренном прямолинейном движении связан с модулями начальной υ 1 и конечной υ 2 скорости и ускорения а выражением \(~s = \frac{\upsilon^2_2 - \upsilon^2_1}{2a}\) .
Отсюда для работы получаем
\(~A = F \cdot s = m \cdot a \cdot \frac{\upsilon^2_2 - \upsilon^2_1}{2a} = \frac{m \cdot \upsilon^2_2}{2} - \frac{m \cdot \upsilon^2_1}{2}\) . (1)
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела .
Кинетическая энергия обозначается буквой E k .
\(~E_k = \frac{m \cdot \upsilon^2}{2}\) . (2)
Тогда равенство (1) можно записать в таком виде:
\(~A = E_{k2} - E_{k1}\) . (3)
Теорема о кинетической энергии
работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.
Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.
Если начальная скорость движения тела массой m равна нулю и тело увеличивает свою скорость до значения υ , то работа силы равна конечному значению кинетической энергии тела:
\(~A = E_{k2} - E_{k1}= \frac{m \cdot \upsilon^2}{2} - 0 = \frac{m \cdot \upsilon^2}{2}\) . (4)
Физический смысл кинетической энергии
кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.
Потенциальная энергия
Потенциальная энергия – это энергия взаимодействия тел.
Потенциальная энергия поднятого над Землей тела – это энергия взаимодействия тела и Земли гравитационными силами. Потенциальная энергия упруго деформированного тела – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Потенциальными называются силы , работа которых зависит только от начального и конечного положения движущейся материальной точки или тела и не зависит от формы траектории.
При замкнутой траектории работа потенциальной силы всегда равна нулю. К потенциальным силам относятся силы тяготения, силы упругости, электростатические силы и некоторые другие.
Силы , работа которых зависит от формы траектории, называются непотенциальными . При перемещении материальной точки или тела по замкнутой траектории работа непотенциальной силы не равна нулю.
Потенциальная энергия взаимодействия тела с Землей
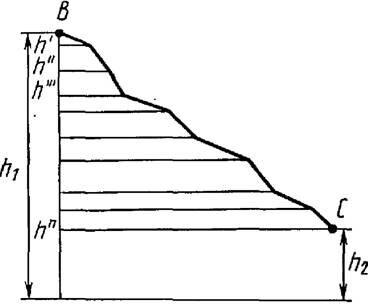
Найдем работу, совершаемую силой тяжести F т при перемещении тела массой m вертикально вниз с высоты h 1 над поверхностью Земли до высоты h 2 (рис. 1). Если разность h 1 – h 2 пренебрежимо мала по сравнению с расстоянием до центра Земли, то силу тяжести F т во время движения тела можно считать постоянной и равной mg .
Так как перемещение совпадает по направлению с вектором силы тяжести, работа силы тяжести равна
\(~A = F \cdot s = m \cdot g \cdot (h_1 - h_2)\) . (5)
Рассмотрим теперь движение тела по наклонной плоскости. При перемещении тела вниз по наклонной плоскости (рис. 2) сила тяжести F т = m∙g совершает работу
\(~A = m \cdot g \cdot s \cdot \cos \alpha = m \cdot g \cdot h\) , (6)
где h – высота наклонной плоскости, s – модуль перемещения, равный длине наклонной плоскости.
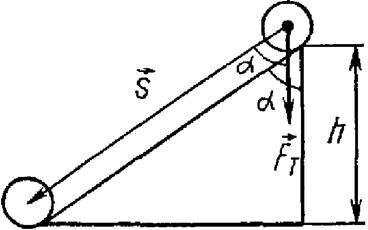
Движение тела из точки В в точку С по любой траектории (рис. 3) можно мысленно представить состоящим из перемещений по участкам наклонных плоскостей с различными высотами h ’, h ’’ и т. д. Работа А силы тяжести на всем пути из В в С равна сумме работ на отдельных участках пути:
\(~A = m \cdot g \cdot h" + m \cdot g \cdot h"" + \ldots + m \cdot g \cdot h^n = m \cdot g \cdot (h" + h"" + \ldots + h^n) = m \cdot g \cdot (h_1 - h_2)\) , (7)
где h 1 и h 2 – высоты от поверхности Земли, на которых расположены соответственно точки В и С .
Равенство (7) показывает, что работа силы тяжести не зависит от траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях.
При движении вниз работа силы тяжести положительна, при движении вверх – отрицательна. Работа силы тяжести на замкнутой траектории равна нулю.
Равенство (7) можно представить в таком виде:
\(~A = - (m \cdot g \cdot h_2 - m \cdot g \cdot h_1)\) . (8)
Физическую величину, равную произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли.
Работа силы тяжести при перемещении тела массой m из точки, расположенной на высоте h 2 , в точку, расположенную на высоте h 1 от поверхности Земли, по любой траектории равна изменению потенциальной энергии взаимодействия тела и Земли, взятому с противоположным знаком.
\(~A = - (E_{p2} - E_{p1})\) . (9)
Потенциальная энергия обозначается буквой Е p .
Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, т. е. высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.
При таком выборе нулевого уровня потенциальная энергия Е p тела, находящегося на высоте h над поверхностью Земли, равна произведению массы m тела на модуль ускорения свободного падения g и расстояние h его от поверхности Земли:
\(~E_p = m \cdot g \cdot h\) . (10)
Физический смысл потенциальной энергии взаимодействия тела с Землей
потенциальная энергия тела, на которое действует сила тяжести, равна работе, совершаемой силой тяжести при перемещении тела на нулевой уровень.
В отличие от кинетической энергии поступательного движения, которая может иметь лишь положительные значения, потенциальная энергия тела может быть как положительной, так и отрицательной. Тело массой m , находящееся на высоте h , где h < h 0 (h 0 – нулевая высота), обладает отрицательной потенциальной энергией:
\(~E_p = -m \cdot g \cdot h\) .
Потенциальная энергия гравитационного взаимодействия
Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами m и М , находящихся на расстоянии r одна от другой, равна
\(~E_p = G \cdot \frac{M \cdot m}{r}\) . (11)
где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Е p = 0) принят при r = ∞.
Потенциальная энергия гравитационного взаимодействия тела массой m с Землей, где h – высота тела над поверхностью Земли, M e – масса Земли, R e – радиус Земли, а нуль отсчета потенциальной энергии выбран при h = 0.
\(~E_e = G \cdot \frac{M_e \cdot m \cdot h}{R_e \cdot (R_e +h)}\) . (12)
При том же условии выбора нуля отсчета потенциальная энергия гравитационного взаимодействия тела массой m с Землей для малых высот h (h « R e) равна
\(~E_p = m \cdot g \cdot h\) ,
где \(~g = G \cdot \frac{M_e}{R^2_e}\) – модуль ускорения свободного падения вблизи поверхности Земли.
Потенциальная энергия упруго деформированного тела
Вычислим работу, совершаемую силой упругости при изменении деформации (удлинения) пружины от некоторого начального значения x 1 до конечного значения x 2 (рис. 4, б, в).

Сила упругости изменяется в процессе деформации пружины. Для нахождения работы силы упругости можно взять среднее значение модуля силы (т.к. сила упругости линейно зависит от x ) и умножить на модуль перемещения:
\(~A = F_{upr-cp} \cdot (x_1 - x_2)\) , (13)
где \(~F_{upr-cp} = k \cdot \frac{x_1 - x_2}{2}\) . Отсюда
\(~A = k \cdot \frac{x_1 - x_2}{2} \cdot (x_1 - x_2) = k \cdot \frac{x^2_1 - x^2_2}{2}\) или \(~A = -\left(\frac{k \cdot x^2_2}{2} - \frac{k \cdot x^2_1}{2} \right)\) . (14)
Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:
\(~E_p = \frac{k \cdot x^2}{2}\) . (15)
Из формул (14) и (15) следует, что работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятому с противоположным знаком:
\(~A = -(E_{p2} - E_{p1})\) . (16)
Если x 2 = 0 и x 1 = х , то, как видно из формул (14) и (15),
\(~E_p = A\) .
Физический смысл потенциальной энергии деформированного тела
потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.
Потенциальная энергия характеризует взаимодействующие тела, а кинетическая энергия – движущиеся тела. И потенциальная, и кинетическая энергия изменяются только в результате такого взаимодействия тел, при котором действующие на тела силы совершают работу, отличную от нуля. Рассмотрим вопрос об изменениях энергии при взаимодействиях тел, образующих замкнутую систему.
Замкнутая система – это система, на которую не действуют внешние силы или действие этих сил скомпенсировано . Если несколько тел взаимодействуют между собой только силами тяготения и силами упругости и никакие внешние силы на них не действуют, то при любых взаимодействиях тел работа сил упругости или сил тяготения равна изменению потенциальной энергии тел, взятому с противоположным знаком:
\(~A = -(E_{p2} - E_{p1})\) . (17)
По теореме о кинетической энергии, работа тех же сил равна изменению кинетической энергии:
\(~A = E_{k2} - E_{k1}\) . (18)
Из сравнения равенств (17) и (18) видно, что изменение кинетической энергии тел в замкнутой системе равно по абсолютному значению изменению потенциальной энергии системы тел и противоположно ему по знаку:
\(~E_{k2} - E_{k1} = -(E_{p2} - E_{p1})\) или \(~E_{k1} + E_{p1} = E_{k2} + E_{p2}\) . (19)
Закон сохранения энергии в механических процессах :
сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и си-лами упругости, остается постоянной.
Сумма кинетической и потенциальной энергии тел называется полной механической энергией .
Приведем простейший опыт. Подбросим вверх стальной шарик. Сообщив начальную скорость υ нач, мы придадим ему кинетическую энергию, из-за чего он начнет подниматься вверх. Действие силы тяжести приводит к уменьшению скорости шарика, а значит, и его кинетической энергии. Но шарик поднимается выше и выше и приобретает все больше и больше потенциальной энергии (Е p = m∙g∙h ). Таким образом, кинетическая энергия не исчезает бесследно, а происходит ее превращение в потенциальную энергию.
В момент достижения верхней точки траектории (υ = 0) шарик полностью лишается кинетической энергии (Е k = 0), но при этом его потенциальная энергия становится максимальной. Дальше шарик меняет направление движения и с увеличивающейся скоростью движется вниз. Теперь происходит обратное превращение потенциальной энергии в кинетическую.
Закон сохранения энергии раскрывает физический смысл понятия работы :
работа сил тяготения и сил упругости, с одной стороны, равна увеличению кинетической энергии, а с другой стороны, – уменьшению потенциальной энергии тел. Следовательно, работа равна энергии, превратившейся из одного вида в другой.
Закон об изменении механической энергии
Если система взаимодействующих тел не замкнута, то ее механическая энергия не сохраняется. Изменение механической энергии такой системы равно работе внешних сил:
\(~A_{vn} = \Delta E = E - E_0\) . (20)
где Е и Е 0 – полные механические энергии системы в конечном и начальном состояниях соответственно.
Примером такой системы может служить система, в которой наряду с потенциальными силами действуют непотенциальные силы. К непотенциальным силам относятся силы трения. В большинстве случаев, когда угол между силой трения F r тела составляет π радиан, работа силы трения отрицательна и равна
\(~A_{tr} = -F_{tr} \cdot s_{12}\) ,
где s 12 – путь тела между точками 1 и 2.
Силы трения при движении системы уменьшают ее кинетическую энергию. В результате этого механическая энергия замкнутой неконсервативной системы всегда уменьшается, переходя в энергию немеханических форм движения.
Например, автомобиль, двигавшийся по горизонтальному участку дороги, после выключения двигателя проходит некоторый путь и под действием сил трения останавливается. Кинетическая энергия поступательного движения автомобиля стала равной нулю, а потенциальная энергия не увеличилась. Во время торможения автомобиля произошло нагревание тормозных колодок, шин автомобиля и асфальта. Следовательно, в результате действия сил трения кинетическая энергия автомобиля не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.
Закон сохранения и превращения энергии
при любых физических взаимодействиях энергия превращается из одной формы в другую.
Иногда угол между силой трения F tr и элементарным перемещением Δr равен нулю и работа силы трения положительна:
\(~A_{tr} = F_{tr} \cdot s_{12}\) ,
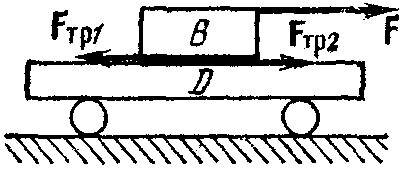
Пример 1 . Пусть, внешняя сила F действует на брусок В , который может скользить по тележке D (рис. 5). Если тележка перемещается вправо, то работа силы трения скольжения F tr2 , действующей на тележку со стороны бруска, положительна:
Пример 2 . При качении колеса его сила трения качения направлена вдоль движения, так как точка соприкосновения колеса с горизонтальной поверхностью двигается в направлении, противоположном направлению движения колеса, и работа силы трения положительна (рис. 6):

Литература
- Кабардин О.Ф. Физика: Справ. материалы: Учеб. пособие для учащихся. – М.: Просвещение, 1991. – 367 с.
- Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. сред. шк. – М.: Про-свещение, 1992. – 191 с.
- Элементарный учебник физики: Учеб. пособие. В 3 т. / Под ред. Г.С. Ландсберга: т. 1. Механика. Теплота. Молекулярная физика. – М.: Физматлит, 2004. – 608 с.
- Яворский Б.М., Селезнев Ю.А. Справочное руководство по физике для поступающих в вузы и самообразования. – М.: Наука, 1983. – 383 с.
Учебная цель: добиться понимания физических понятийэнергии, работы, мощности и закона сохранения энергии. Привить навыки самостоятельного решения задач по данной теме.
Литература
Основная: Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 1989. – Гл. 3, § 3.1 – 3.4; гл. 5, § 5.2.
Дополнительная: Савельев И.В. Курс общей физики. – М.: Наука, 1987. – Т. 1, гл. 3, § 19 – 24.
Контрольные вопросы для подготовки к занятию
1. Поясните физический смысл понятий энергии, работы, мощности. Их единицы измерения.
2. Какие виды механической энергии известны? Чем они определяются?
3. Запишите и объясните формулы кинетической энергии поступательного и вращательного движения тела.
4. Каковы способы определения работы?
5. Как определяется работа сил упругой деформации и потенциальная энергия упруго деформированного тела?
6. По какой формуле можно определить потенциальную энергию гравитационного взаимодействия двух материальных точек (шаров)? Поясните, почему она является отрицательной величиной?
7. Дайте определение консервативной и диссипативной систем тел. Приведите примеры.
8. Сформулируйте, поясните и запишите закон сохранения энергии в механике.
Краткие теоретические сведения и основные формулы
Энергия – универсальная мера различных форм движения и взаимодействия всех видов материи.
Механическая энергия может быть обусловлена двумя причинами:
Движением тела с некоторой скоростью (кинетическая энергия);
Нахождением тела в потенциальном поле сил (потенциальная энергия).
Кинетическая энергия тела массой m , движущегося поступательно со скоростью
Кинетическая энергия вращающегося вокруг неподвижной оси тела
Потенциальная энергия тяготения двух материальных точек, массы которых и, находящихся на расстоянииr , при условии, что W = 0, равна
где G = 6,67·10 -11 –гравитационная постоянная . Знак минус соответствует тому, что при r потенциальная энергия двух взаимодействующих тел равна нулю; при сближении этих тел потенциальная энергия убывает.
Потенциальная энергия сил притяжения всегда является отрицательной. Область пространства, где действуют силы притяжения, называется потенциальной ямой.
Потенциальная энергия тела, поднятого на высоту h относительно тела отсчёта (например, Земли)
W n = m g h ,
где g = 9,81 – ускорение свободного падения.
Потенциальная энергия упруго деформированного тела
где -коэффициент упругости , определяемый отношением упругой силы к величинеупругой деформации.
Закон сохранения энергии в механике: полная механическая энергия замкнутой системы, в которой действуют только консервативные силы, есть величина постоянная, т.е.
W k + W n = сonst.
Системы, в которых полная механическая энергия не сохраняется, называются диссипативными.
Мерой передачи движения, или мерой энергии, переданной от одного тела к другому, является работа .
На основании определения работы изменение полной механической энергии системы равно алгебраической сумме работ всех внешних и внутренних сил:
A = W 2 – W 1 Дж,
где W 2 и W 1 – полные энергии тел соответственно после и до взаимодействия.
При упругой деформации стержня сила , приложенная к стержню, совершает работу:
 (3.50)
(3.50)
Преобразуем это выражение так, чтобы в него вошли параметры деформируемого тела вместо жесткости . Для этого подставим в выражение закона Гука относительную деформацию и механическое напряжение :
Из (3.51) следует, что
 , (3.52)
, (3.52)
 (3.53)
(3.53)
Работа внешней силы идет на увеличение запаса потенциальной энергии деформированного тела: . Если стержень однородный, то его деформация равномерно распределена по объему стержня. Тогда энергию деформации также можно считать равномерно распределенной по объему стержня, с плотностью энергии упругой деформации:
![]() . (3.54)
. (3.54)
ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Рассмотрим теперь общий случай: пусть имеется система из частиц, взаимодействующих между собой посредством консервативных сил, и одновременно находящихся под действием внешних консервативных и неконсервативных сил.
Получим выражение для работы, совершаемой над частицами системы, при перемещении системы из одного положения в другое и одновременном изменении конфигурации системы. Обозначим работу внешних консервативных сил . Эта работа равна убыли потенциальной энергии во внешнем поле сил:
![]() . (3.55)
. (3.55)
Для работы внутренних консервативных сил при изменении конфигурации системы справедливо аналогичное выражение:
Обозначим работу неконсервативных сил . Вспомним, сформулированное нами ранее утверждение: суммарная работа идет на приращение кинетической энергии системы . Тогда можно записать соотношение:
Подставим в левую часть выражения для работы консервативных сил:
Или, после перегруппировки слагаемых по индексам,
Обозначим сумму ![]() . Эта сумма, по определению, представляет собой полную механическую энергию системы
. Тогда из (3.54) следует, что приращение полной энергии системы
. Эта сумма, по определению, представляет собой полную механическую энергию системы
. Тогда из (3.54) следует, что приращение полной энергии системы
![]() (3.55)
(3.55)
равно работе не консервативных сил.
В частном случае, при их отсутствии , полная энергия не изменяется:
Таким образом, полная механическая энергия системы материальных точек, находящихся под действием только консервативных сил, остается постоянной . Это утверждение называют законом сохранения механической энергии .
УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
Рассмотрим частицу, на которую действуют только консервативные силы. Если в некотором состоянии результирующая сил, действующих на частицу равна нулю, то говорят, что частица находится в состоянии равновесия . В зависимости от последствий незначительного отклонения системы от положения равновесия различают:
§ устойчивое равновесие – если возникают силы, возвращающие систему в положение равновесия (рисунок 2.3 – 1);
- неустойчивое равновесие – если возникают силы, удаляющие систему от равновесия (рисунок 2.3 – 2);
- безразличное равновесие – если в новом положении система также оказывается в положении равновесия (рисунок 2.3 – 3).
![]()
ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА.
ЦЕНТР МАСС И ЕГО ДВИЖЕНИЕ
Вторым аддитивным интегралом движения, сохраняющимся для замкнутой системы является её импульс .
Рассмотрим систему взаимодействующих частиц. На i -тую частицу системы действуют внутренние силы и внешне с результирующей . Уравнение движения i -той частицы имеет вид:
 (3.57)
(3.57)
Аналогичные уравнения, очевидно можно записать для каждой из частиц. Сложив левые и правые части уравнений, получим
 (3.58)
(3.58)
Двойная сумма в (3.58) представляет собой сумму всех внутренних
сил системы. По третьему закону Ньютона , и для каждого слагаемого в этой сумме найдется противоположный ему вектор. Поэтому  .
.
По определению импульсом системы называютвекторную сумму импульсов тел системы , т.е. величину . Таким образом, в левой части (3.58) стоит производная импульса системы. Если система замкнута, то из (3.58) следует, что
 (3.58)
(3.58)
Таким образом, импульс замкнутой системы материальных точек остается постоянным . Это утверждение называют законом сохранения импульса .
Требование отсутствия внешних сил не является жестким. Если в пространстве существует такое направление, что проекция суммы результирующих внешних сил на него равна нулю, то, в соответствии с (3.58), проекция импульса системы на это направление будет оставаться постоянной.
Важным свойством обладает точка, называемая центром масс системы . Если система образована материальными точками с массами , а их положение задается радиус-векторами
Потенциальной энергией может обладать не только система взаимодействующих тел, но и отдельно взятое упруго деформированное тело (например, сжатая пружина, растянутый стержень и т. п.). В этом случае потенциальная энергия зависит от взаимного расположения отдельных частей тела (например, от расстояния между соседними витками пружины).
Согласно формуле (20.2) как для растяжения, так и длясжатия пружины на величину я необходимо затратить работу . Эта работа идет на увеличение потенциальной энергии пружины. Следовательно, зависимость потенциальной энергии пружины от удлинения х имеет вид
где - коэффициент жесткости пружины (см. § 14). Формула (25.4) написана в предположении, что потенциальная энергий недеформнированной пружины равна нулю. На рис. 25.1 показан график зависимости U от х.

При упругой продольной деформации стержня совершается работа, определяемая формулой (20.3). В соответствии с этим потенциальная энергия упруго деформированного стержня равна
Здесь Е - модуль Юнга, - относительное удлинение, - объем стержня;
Введем в рассмотрение плотность энергии упругой деформации и, которую определим как отношение энергии dU к тому объему в котором она заключена:
Поскольку стержень предполагается однородным и деформация, является равномерной, т. е. одинаковой в разных точках стержня, энергия (25.2) распределена в стержне также равномерно. Поэтому можно считать, что
![]()
Это выражение дает плотность энергии упругой деформации при растяжении (или сжатии) и в том случае, когда деформация неравномерна. В последнем случае для нахождения плотности энергия в «некоторой точке Стержня нужно подставлять в (25.4) значение в данной точке.

